Home
Correlations of Random Binary Sequences with Pre-Stated Operator Intention

Correlations of Random Binary Sequences with Pre-Stated Operator Intention

A Review of a 12-Year Program , by R. G. Jahn, B. J. Dunne, R. D. Nelson, Y. H. Dobyns, and G. J. Bradish

Le PEAR (Princeton Engineering Anomalies Research) a été fondé en 1979 à l’initiative de Robert G. Jahn, alors doyen de la faculté d’ingénierie et de sciences appliquées de l’université de Princeton. Ce laboratoire d’ingénierie, toujours en activité, propose une approche qui se distingue d’une démarche parapsychologique « classique » car elle est tournée plus spécifiquement vers des aspects physiques et techniques.
Les chercheurs du PEAR ont ainsi mené des expériences originales, en particulier sur la psychokinèse, en étudiant d’éventuelles influences de sujets sur des Générateurs de Nombres aléatoires (GNA), mais aussi en utilisant des systèmes moins conventionnels, comme des cascades mécaniques aléatoires (RMC experiments), des pendules, ou encore des franges d’interférence.
Cet article expose les résultats accumulés au cours de 12 années d’expériences de micro-psychokinèse au sein de ce laboratoire. Son principal intérêt réside dans la quantité importante des données étudiées, permettant ainsi de mettre à jour un certain nombre de caractéristiques des phénomènes observés.

________

 

Princeton Engineering Anomalies Research (PEAR)
School of Engineering and Applied Science, Princeton University

NB: This is a reprint of an essay originally published in the Journal of Scientific Exploration, Vol. 11, No. 3, pp. 345-367, 1997.

Abstract — Strong correlations between output distribution means of a variety of random binary processes and prestated
intentions of some 100 individual human operators have been established over a 12-year experimental
program. More than 1000 experimental series, employing four different categories of random devices and several
distinctive protocols, show comparable magnitudes of anomalous mean shifts from chance expectation, with similar
distribution structures. Although the absolute effect sizes are quite small, of the order of10-4bits deviation per bit processed, over the huge databases accumulated the composite effect exceeds 7σ(p= 3.5 × 10-13). These data
display significant disparities between female and male operator performances, and consistent serial position effects
in individual and collective results. Data generated by operators far removed from the machines and exerting their
efforts at times other than those of machine operation show similar effect sizes and structural details to those of the
local, on-time experiments. Most other secondary parameters tested are found to have little effect on the scale and
character of the results, with one important exception: studies performed using fully deterministic pseudorandom
sources, either hard-wired or algorithmic, yield null overall mean shifts, and display no other anomalous features.

I. Background

The role of human consciousness in the establishment of physical reality has been debated in
many contexts and formats throughout every era of scientific history. The issue was central to
ancient Egyptian and Greek philosophy, and to the enduring Hermetic tradition from which
classical empirical science emerged. Even well into the period of scientific enlightenment,
scholars of the stature of Francis Bacon [[Walker, D. P. (1972). “Francis Bacon and Spiritus.” In A. G. Debus, ed., Science, Medicine and
Society in the Renaissance. New York: Neale Watson Academic Publications, Inc., Science
History Publications.]], Robert Hooke [[Hooke, R. (1976). In R. Waller, ed., The posthumus works of Robert Hooke, M.D., S.R.S.,
containing his Cutlerian lectures and other discourses, read at the meetings of the illustrious
Royal Society (London: Smith and Walford [Printers to the Royal Society], 1705), p. 147.
(Quoted in B. R. Singer, “Robert Hooke on Memory, Association, and Time Perception,” in R. V.
Jones and W. D. M. Paton, eds., Notes and Records of the Royal Society of London, Vol. 31, No.
1, p. 123.).]], Robert Boyle [[Boyle, R. (1962). Works, Vol. 1, p. cxxx. (Quoted in L. T. Moore, Newton: A Biography, New
York: Dover Publications.).]], and Isaac
Newton [[Kubrin, D. (1981). “Newton’s Inside Out! Magic, Class Struggle, and the Rise of Mechanism in
the West.” In H. Woolf, ed., The Analytic Spirit: Essays in the History of Science. Ithaca and
London: Cornell University Press.]] addressed many of their empirical investigations to “the mystery by which mind
could control matter” [[Ibid., p. 113.]]. Although the maturing scientific establishment of the following two
centuries came largely to dismiss such possibility, a number of distinguished physicists,
including J. J. Thompson, William Crookes, Lord Rayleigh, and Marie and Pierre Curie
continued to regard this topic as relevant to their scholarship, and were active participants in the
Society for Psychical Research [[Beloff, J. (1977). “Historical Overview”. In B. B. Wolman, ed., Handbook of Parapsychology. New
York: Van Nostrand Reinhold Co.]]. A subtler form of the question arose in the early
“observational” interpretations of quantum mechanics which were construed by a number of the
patriarchs of modern physics, including Planck [[Planck, M. (1932). Where Is Science Going? (trans. J. Murphy). New York: W. Norton & Co.]], Bohr [[Bohr, N. (1961). Atomic Theory and the Description of Nature. Cambridge: University Press.]], Schrödinger [[Schrödinger, E. (1967). What Is Life? and Mind and Matter. Cambridge: University Press.]], de Broglie [[de Broglie, L. (1955). Physics and Microphysics (trans. M. Davidson). New York: Pantheon
Books.]],
Heisenberg [[Heisenberg, W. (1962). Physics and Philosophy: The Revolution in Modern Science. New York:
Harper and Row (Harper Torchbooks).]], Pauli [[Pauli, W. (1994). “Ideas of the Unconscious.” In C. P. Enz and K. von Meyenn, eds., Wolfgang
Pauli: Writings on Physics and Philosophy (trans. R. Schlapp). Berlin, Heidelberg: Springer-
Verlag.]], Einstein [[Schilpp, P. A., ed. (1949). Albert Einstein: Philosopher-Scientist. Evanston, IL: The Library of
Living Philosophers, Inc. (George Banta Publishing Co., Menasha, W. I.).]], Jeans [[Jeans, J. (1943). Physics and Philosophy. Cambridge: University Press.]], Eddington [[Eddington, A. (1978). The Nature of the Physical World. Ann Arbor, MI: University of
Michigan Press.]], Wigner [[Wigner, E. P. (1967). Symmetries and Reflections. Bloomington and London: Indiana University
Press.]], Jordan [[Jordan, P. (1960). Parapsychological implications of research in atomic physics. International
Journal of Parapsychology, Vol. 2, No. 4, p. 5.]],
and von Weizsäcker [[von Weizsäcker, C. F. (1980). The Unity of Nature (trans. F. J. Zucker). New York: Fauar,
Straus, Giroux, Inc]], to raise important questions of the implicit or explicit role of human
consciousness in the collapse of the wave function. Although they vigorously debated such
possibilities from both scientific and philosophical perspectives, little consensus was reached,
other than the need for better direct experimentaldata.Theenigma of consciousness continues to interest some contemporary physicists in such
contexts as the non-locality/EPR paradox/Bell’s theorem debates [[Kafatos, M., ed. (1989). Bell’s Theorem, Quantum Theory and Conception of the Universe.
Heidelberg: Klewer Academic Press.]], single photon interference
[[Clauser, J. F. (1974). Experimental distinction between the quantum and classical field-theoretic
predictions for the photoelectric effect. Physical Review D, Vol. 9, No. 4, p. 853.]], causality violations in thermodynamics [[Donald, J. A. & Martin, B. (1976). Time-symmetric thermodynamics and causality violation.
European Journal of Parapsychology, Vol. 1, No. 3, p. 17.]], neurophysics [[Shear, J., ed. (1996). Controversies in science and the humanities: Exploring consciousness-the
“hard problem.” Journal of Consciousness Studies, Special issue, Part II, Vol. 3, No. 1.]], complexity and chaos
theory [[Atmanspacher, H. & Dalenoort, G. J., eds. (1994). Inside versus Outside: Endo- and Exo-
Concepts of Observation and Knowledge in Physics, Philosophy and Cognitive Science. Berlin:
Springer-Verlag.]], and numerous other aspects of quantum epistemology and measurement [[Hiley, B. J. & Peat, F. D., eds. (1987). Quantum Implications: Essays in Honour of David Bohm.
London and New York: Routledge & Kegan Paul.]][[Schommers, W., ed. (1989). Quantum Theory and Pictures of Reality: Foundations,
Interpretations, and New Aspects. Berlin, Heidelberg: Springer-Verlag.]],
once again without much resolution. Indeed, although a myriad of theoretical and empirical
attempts have been made to define the elusive concept of consciousness itself, curiously little
agreement on its origins, substance, characteristics, or functions has yet been achieved. Some of
these efforts relegate consciousness to a complex of emergent phenomena of the human brain,
and thus to an ensemble of neurochemical and neuroelectrical processes [[Scott, A. (1995). Stairway to the Mind: The Controversial New Science of Consciousness. New
York: Springer-Verlag (Copernicus).]] [[Borstner, B. & Shawe-Taylor, J. (1995). Consciousness at the Crossroads of Philosophy and
Cognitive Science: Selected Proceedings of the final meeting of the Tempus Project
‘Phenomenology and Cognitive Science,’ Maribor, Slovenia, 23-27 August, 1994 and
Consciousness Research Abstracts ‘Toward a Scientific Basis for Consciousness’ (Tucson I):
Classifed Abstracts of the Conference, The University of Arizona, Tucson AZ, USA, April 12-17
1994. Thorverton, UK: Imprint Academic.]]. Others attempt
to invoke quantum indeterminacy in explication of brain function [[Stapp, H. P. (1993). Mind, Matter, and Quantum Mechanics. Berlin: Springer-Verlag.]]. While many
philosophers of science maintain that the concept of consciousness is so intrinsically subjective
that it must be excluded from scientific attention, others plead that scientific scholarship cannot
indefinitely ignore such dimensions [[Jahn, R. G., ed. (1981). The Role of Consciousness in the Physical World: AAAS Selected
Symposium 57. Boulder, CO: Westview Press, Inc.]].
Earlier in this century, attempts to codify the psychological dimensions of the problem
were undertaken by a community of “parapsychologists” rooted in the pioneering research of
J. B. and Louisa Rhine [[Rhine, J. B. et al. (1965). Parapsychology from Duke to FRNM. Durham, NC: The
Parapsychology Press.]]. In most such studies, the consciousness aspect hypothesized to
correlate with the behavior of physical systems entailed some form of volition, intention, or
desire, a presumption consistent with the premises of most religions, mystical traditions, personal
superstitious practices, and the innate human propensity to hope or to wish. Portions of this early
work attracted the attention of Pauli [[Pauli, W. (1994). “Ideas of the Unconscious.” In C. P. Enz and K. von Meyenn, eds., Wolfgang
Pauli: Writings on Physics and Philosophy (trans. R. Schlapp). Berlin, Heidelberg: Springer-
Verlag, pp. 149-164.]] and other quantum physicists. Einstein reports on a
conversation he held with “an important theoretical physicist” regarding the relevance of Rhine’s
research to the EPR paradox:

He: I am inclined to believe in telepathy.I: This has probably more to do with physics than with psychology.He: Yes.– [[Schilpp, P. A., ed. (1949). Albert Einstein: Philosopher-Scientist. Evanston, IL: The Library of
Living Philosophers, Inc. (George Banta Publishing Co., Menasha, W. I.), p. 683.]]

Notwithstanding this interest, much of the subsequent research of this genre proved vulnerable to
technical criticism and unpersuasive to the scientific mainstream.
Most recently, the more sophisticated information processing technology that has
advanced our understanding of the physical world over the last half century has also provided
tools for addressing this class of anomalous phenomena with a methodological rigor
unimaginable in the earlier parapsychological research. For example, over the period 1959 to
1987, some 832 experimental studies conducted by 68 investigators directly addressed the
influence of human intention on the performance of a broad variety of random event generators.
Meta-analytical assessment of these results yields strong statistical evidence for small but
consistent anomalous effects that correlate with the intentions or desires of their operators [[Radin, D. I. & Nelson, R. D. (1989). Evidence for consciousness-related anomalies in random
physical systems. Foundations of Physics, Vol. 19, No. 12, p. 1499.]],
raising possible implications for experimental and theoretical study of many other probabilistic
physical events, and for their technological applications. At the least, these findings should
motivate performance and contemplation of yet more precise and extensive empirical studies.
The purpose of this article is to present a major body of new data that bears on this issue,
acquired over twelve years of experimental study of anomalous human/machine interactions,
conducted in an engineering laboratory context. Specifically, these studies have searched for
possible correlations between the output data distributions of various random binary processes
and the pre-stated intentions of attendant human operators. The history of this laboratory
program, details of its instrumentation, protocols, data reduction and interpretation techniques,
its attempts to model the observed effects, and the possible implications of the results for various regimes of basic science and technical applications have been described elsewhere [[Jahn, R. G. & Dunne, B. J. (1988). Margins of Reality: The Role of Consciousness in the
Physical World. New York, San Diego: Harcourt Brace Jovanovich.]][[Jahn, R. G. (1982). The persistent paradox of psychic phenomena: An engineering perspective.
Proceedings of the IEEE, Vol. 70, No. 2, p. 136.]][[Jahn, R. G., Dunne, B. J., and Nelson, R. D. (1987). Engineering anomalies research. Journal of
Scientific Exploration, Vol. 1, No. 1, p. 21.]][[Jahn, R. G. & Dunne, B. J. (1986). On the quantum mechanics of consciousness, with application
to anomalous phenomena. Foundations of Physics, Vol. 16, No. 8, p. 721.]][[Jahn, R. G. (1998). Physical aspects of psychic phenomena. Physics Bulletin, Vol. 9, p. 235.]].
Here we shall focus only on the empirical results and their individual and collective statistical
merit.

II. Equipment and Protocol

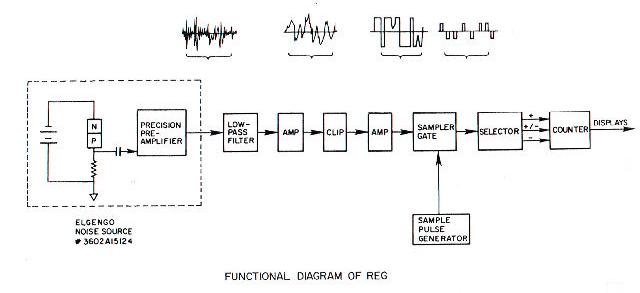
The machine employed in the “benchmark” experiments of this program is a
microelectronic random event generator (REG) driven by a commercial noise board (Elgenco
#3602A – 15124), involving a reverse-biased semi-conductor junction, precision preamplifiers,
and filters. The output spectrum of this noise source, essentially constant (± 1 db) from 50 Hz to
20 kHz, is clipped and further amplified to provide a randomly alternating flat-topped wave form
of ± 10 volt amplitude with 0.5 μsec rise and fall times which is gate-sampled at selectable
regular intervals to yield a randomly alternating sequence of positive and negative pulses. A set
number of these are then counted against a regularly alternating +,-,+,-,… template, thereby
differentially eliminating any distortion of randomicity due to ground reference drift. The
immediate and cumulative results are displayed via LEDs on the machine face and graphically
on a computer screen, and transmitted on-line to a data management system. The balance of the
device entails a variety of voltage and thermal monitors, redundant counters, and other fail-safe
features that ensure its nominal operation and preclude tampering, and other security features are
incorporated in the operational software. The machine is extensively and frequently calibrated in
unattended operation, and is invariably found to reproduce the theoretical binomial combinatorial
distributions having the appropriate means and standard deviations, with all higher moments and
sequential correlations negligible, to statistical confidence more than adequate to support the
claimed experimental correlations. A block diagram of this REG is shown in Figure 1; further
technical details are available upon request.
For the benchmark experiments, this REG is set to generate trials of 200 binary samples
each, which are counted at a rate of 1000 per second. The protocol requires individual human
operators, seated in front of the machine but having no physical contact with it, to accumulate
prescribed equal size blocks of data under three interspersed states of intention: to achieve a
higher number of bit counts than the theoretical mean (HI); to achieve a lower number of bit
counts than the theoretical mean (LO); or not to influence the output, i.e., to establish a baseline
(BL). Data are collected in runs of 50, 100, or 1000 trials, depending on operator preference and
protocol variations, and compounded over some number of experimental sessions into predefined
data series of a specified number of trials, ranging from 1000 to 5000 per intention. Data
processing is performed at the level of these individual series, which are regarded as the basic
experimental units for interpretation and replication of any results. The essential criteria for
anomalous correlations are statistically significant departures of the HI and/or LO series mean
scores from the theoretical chance expectation and, most indicatively, the separation of the highand
low-intention data (HI–LO).

Fig. 1.

III. Primary Results

A. Collective Mean Shifts

Over a 12-year period of experimentation, 91 individual operators, all anonymous,
uncompensated adults, none of whom claimed unusual abilities, accumulated a total of 2,497,200
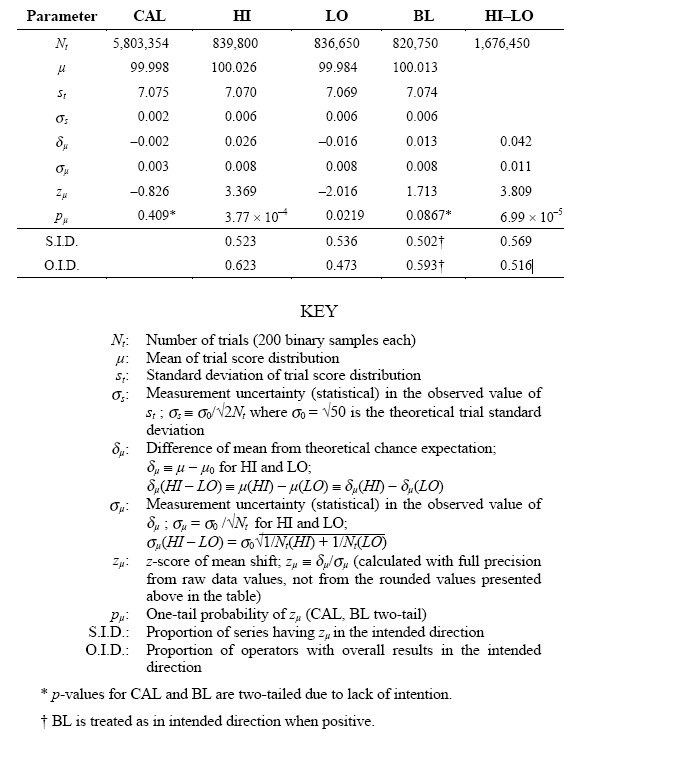
trials distributed over 522 tripolar series in this benchmark experiment. Table 1 lists the overall
results for the three categories of intention, HI, LO, and BL, and for the HI-LO separations, for
comparison with the concomitant calibration data and the theoretical chance expectations. With
reference to the symbol list below the table, the salient indicators are the mean shifts from the
theoretical expectation,δμ, the corresponding z-scores, zμ, and the one-tail probabilities of chance
occurrence of these or larger deviations, pμ. Also listed are the proportions of the 522 series
yielding results in the intended directions, S. I. D., and the proportions of operators achieving
results in the intended directions, O. I. D. (Note that as defined,δμis expressed in units of
bits/trial. We could equally well represent the effect size in absolute units of bits/bit processed,
i.e., εμ = δμ/2μ0, which in turn differs by a factor of two from the common statistical effect size, zμ/

$\sqrtN_b$

) =δμ/μ0, where Nb denotes the total number of bits processed. We shall henceforth use δμ and εμ more or less interchangeably, as befits the context.)
The measures tabulated in Table 1 individually and collectively define the scale and
character of the primary anomaly addressed in these studies, i.e., the statistically significant
correlations of the output of this microelectronic random binary process with the pre-recorded
intentions of a large pool of unselected human operators. Specifically to be noted is the overall
scale of the effect,O(10-4)bits inverted per bit processed; the somewhat higher deviation in the HI results compared to the LO; the slight departure of the BL results from both the theoretical
chance expectation and the calibration value, and the negligible alterations in the variances of the
score distributions. The overall figure of merit for the HI-LO separation, which is the postulated
primary indicator, iszμ = 3.81 (pμ = 7 × 10-5).
The anomalous correlations also manifest in the fraction of experimental series in which
the terminal results confirm the intended directions. For example, 57% of the series display HI-LO score separations in the intended direction(zs = 3.15, ps = 8 × 10-4).In contrast, the anomaly
is not statistically evident in the 52% of individual operators producing databases in the intended
directions(z0 = 0.31, p0 = 0.38), a feature having possible structural implications, as discussed below.

TABLE 1

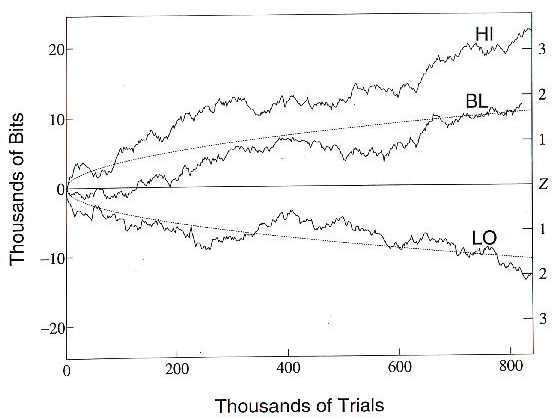
B. Cumulative Deviations

An instructive alternative display of these results is in the form of cumulative deviation graphs, wherein are plotted the accumulating total departures from the chance mean sequentially compounded by this group of operators in their HI, LO, and BL efforts over the long history of the experiment (Figure 2). The superimposed parabolic envelopes indicate the increasing width of one-tailed 95% confidence intervals about the theoretical mean as the database evolves. In this format, the deviant trends in the HI and LO performances appear as essentially random walks about shifted mean values, leading to steadily increasing departures from expectation. Consistent with the terminal values listed in Table 1, the average slopes of these two patterns of achievement, in units of bits deviation per bit processed, are roughly1.3 × 10-4 and -7.8 × 10-5 respectively. Although local segments reflective of individual operators or particular periods of operation may differ somewhat from these overall effect sizes, as described below, this10-4 order of magnitude tends to characterize virtually all of the anomalous correlations achieved in these experiments.

Fig. 2.

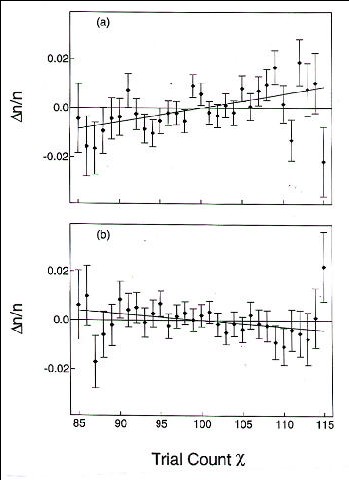
C. Count Distributions

Any structural details of the trial count distributions that compound to the observed
anomalous mean shifts may hold useful implications for modeling such correlations. While no
statistically significant departures of the variance, skew, kurtosis, or higher moments from the
appropriate chance values appear in the overall data, regular patterns of certain finer scale
features can be discerned. For example, deviations of the trial count populations,ni, from their theoretical chance values,nio, conform to statistical linear regressions of the formΔni/nio = 4εμ(χi

μ0) where ci denotes the given trial count (e.g.100, 102, 94, etc.),μ0is the theoretical chance mean of the full distribution (100), and4εμis the slope of the linear regression fit. Figure 3 depicts this effect graphically for the database of Table 1 and Figure 2. Such functional behavior is consistent with a simple displacement of the chance Gaussian distribution to the observed mean value or, equivalently, to a shift in the elementary binomial probability from the exact theoretical value of 0.5 to (0.5 +εμ) [[Jahn, R. G., Dobyns, Y. H., and Dunne, B. J. (1991). Count population profiles in engineering anomalies experiments. Journal of Scientific Exploration, Vol. 5, No. 2, p. 205.]]. Given the consistency of all other features of the distributions with chance expectation, this suggests that the most parsimonious model of the anomalous correlation is between operator intention and the binary probability intrinsic to the experiment.

Fig. 3.

D. Individual Operator Effects

Given the correlation of operator intentions with the anomalous mean shifts, it is
reasonable to search the data for operator-specific features that might establish some pattern of
individual operator contributions to the overall results. Unfortunately, quantitative statistical
assessment of these is complicated by the unavoidably wide disparity among the operator
database sizes, and by the small signal-to-noise ratio of the raw data, leaving graphical and
analytical representations of the distribution of individual operator effects only marginally
enlightening. For example, Figure 4 deploys the 91 individual operator HI-LO mean shift separations as a function of their various database sizes. Superimposed are the theoretical mean
value, the mean value of the composite data, and the1.64σ (pμ= 0.05) deviation loci with
respect to these two means. Of interest here are the ratios of positive and negative points about
the theoretical and empirical means, their dependence on database size and on operator gender,
and the positions and genders of the outliers.
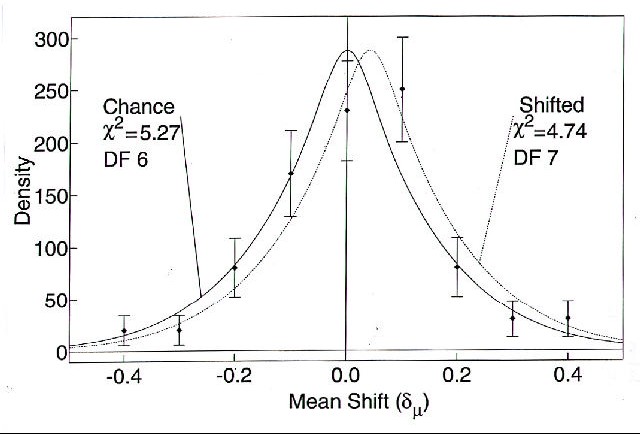
The limited number of operator data points make density plots of these mean shift data
sensitive to the bin sizes and locations selected, but Figure 5 compares one such display with
appropriate theoretical distributions centered on the chance and empirical mean values. The
attached chi-squared values indicate some preference for the latter model, but for these data the
directzμcalculation underlying Table 1 is a far more accurate indicator of the anomalous mean
shift. Attempts to interpret the operator distribution of z-scores, rather than mean shifts, suffer
from the same limitations of available data points, and are similarly inconclusive.
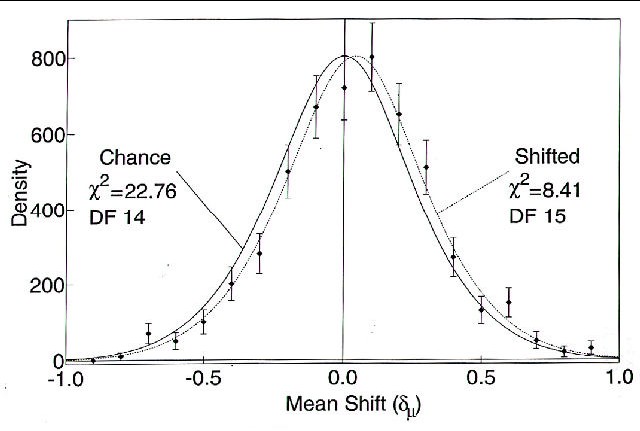
Given the specification of the experimental series as the pre-established unit for data
interpretation, and the significantly larger fraction of series having HI-LO differences in the
intended directions (Table 1), it is also reasonable to search for indications of data structure in
the distribution of series scores achieved by all operators. Since a total of 522 such data units are
available, the resolution of mean shift and z-score distributions is considerably better here, but as
shown in Figure 6, beyond more clearly confirming the overall shifts of the mean, further identification of structural detail remains speculative. This situation is further confused by the
obvious operator gender disparity in the data, as highlighted in the inset table on Figure 4, and
discussed below.

Fig. 5.

IV. Secondary Correlations

Possible secondary correlations of effect sizes with a host of technical, psychological, and
environmental factors, e.g. the type of random source; the distance of the operator from the
machine; operator gender; two or more operators attempting the task together; feedback modes;
the rate of bit generation; the number of bits sampled per trial; the number of trials comprising a
run or series; the volitional/instructed protocol options; the degree of operator experience; and
others have been explored to various extents within the course of these experiments, and in many
other related studies not discussed here. Very briefly, qualitative inspection of these data, along
with a comprehensive analysis of variance [[Nelson, R. D., Dobyns, Y. H., Dunne, B. J., and Jahn, R. G. (1991). “Analysis of Variance of
REG Experiments: Operator Intention, Secondary Parameters, Database Structure.” Technical
Report PEAR 91004, Princeton Engineering Anomalies Research, School of Engineering/
Applied Sciences, Princeton University.]], indicates that most of these factors do not
consistently alter the character or scale of the combined operator effects from those outlined
above, although some may be important in certain individual operator performance patterns. The
few potentially important exceptions to this generalization that have been identified are described
in the following paragraphs.

Fig. 6.

A. Gender-Related Effects

Segregation of the total REG database described above into male and female operator
components reveals several striking disparities. As evident in Figure 4, although three of the
female operators have produced the largest individual z-scores, the overall correlations of mean
shifts with intention are much weaker for the females than for the males. In fact, while a
majority of the males succeed in both directions of effort, most of the females’ low intention
results are opposite to intention. Specifically, some 66% of the male operators succeed in
separating their overall HI and LO scores in the intended direction, compared to only 34% of the
females. In other words, there is some indication that the total operator performance distribution
has three components: a) three outstanding female datasets; b) 38 female datasets indistinguishable
from a chance distribution; and c) 50 well-distributed male datasets compounding to
significant positive performance. Many other aspects of the gender-related disparities are
detailed in Ref. [[Dunne, B. J. (1998). Gender differences in human/machine anomalies experiments. Journal of
Scientific Exploration, Vol. 12, No. 1, pp. 3-55.]].

B. Device Dependence

The sensitivity of the anomalous correlations to the particular random source employed
or to its form of implementation into an experimental device has been extensively explored via a
variety of machines and protocols [[<36>]][[<40>]][[<41>]]. In the simplest variants, the commercial
microelectronic noise diode in the benchmark configuration was replaced by identical and
similar units, with no detectable changes in the character of the results. In a more substantial
and, as it turned out, more critical set of modifications, the physical noise source was replaced by
three distinctly different pseudorandom sources:

  1. A pseudorandom-number generating algorithm included in the Borland Turbo Basic programming package was implemented on an IBM AT-286 computer to provide binary strings that could be counted and displayed in the same formats as the benchmark experiments. More specifically, the floating-point numbers provided by the Borland function, which distribute uniformly over the interval 0 to 1, were converted into bits by assigning 1 to all values above 0.5, and 0 to all values below or equal to 0.5. The initiating seeds were obtained by starting a microsecond clock when the operator prompts first appeared on the screen, and stopping it when the operators responded by pressing a key. The accumulated values were then added to the number of seconds since midnight to compound the seeds. In performing these experiments, the operators had the options of digital, digital cumulative, or graphical cumulative deviation displays on the monitor, akin to those available on the benchmark version.
  2. The benchmark equipment was modified to allow replacement of the Elgenco noise
    source by a hard-wired electronic shift register containing 31 flip-flops comprising a
    sequence length of over2 × 10

    6

    steps. This generator produced strictly deterministic
    sequences from the same initial seed that, at a sampling rate of 1000 Hz, recycled
    roughly every 60 hours, far exceeding the length of any single experimental session.
    From the operator’s perspective, all other aspects of the protocol, machine operation,
    and feedback display were identical to those of the benchmark experiments.

  3. A random element was overlaid on the pseudorandom processor just described by
    introducing an asynchronous shift frequency for the register, driven by an analog
    element that swept from a few kHz to a few tens of kHz over a period of several
    minutes. This unpredictable component of the sampling imbued the device with a
    complex combination of random and pseudorandom characteristics.

As discussed further below, when source #3, which retains some physically random features, is
utilized, statistically significant correlations of results with operator intention, comparable to
those seen in the benchmark experiments, continue to appear. For the strictly deterministic
sources #1 and #2, however, no such correlations are observed.
A more substantial extension of the experimental concept employs a large-scale
mechanical device called a “Random Mechanical Cascade” (RMC), in which 9000×¾ » dia.
polystyrene spheres trickle downward through a quincunx array of 330×¾ » dia. nylon pegs,
whereby they are scattered into 19 collection bins in a close approximation to a Gaussian
population distribution. In this experiment, operators endeavor to shift the mean bin population
to the right or left, or to exert no intention in randomly interspersed trials. The large databases
from this experiment display a similar size and character of anomalous correlations to those of
the smaller-scale random source experiments, and similar count population and other structural
details [[Dunne, B. J., Nelson, R. D., and Jahn, R. G. (1990). Operator-related anomalies in a random
mechanical cascade. Journal of Scientific Exploration, Vol. 2, No. 2, p. 155.]].

C. Series Position Effects

While it might be reasonable to expect that operators’ proficiency at these experimental
tasks would improve with increasing experience, no systematic learning tendencies are evident in
the data. Rather, the progression of the anomalous effect sizes as a function of the number of
series completed by the operators is found to take the somewhat unanticipated form shown in
Figure 7. Namely, when the mean shifts obtained by all operators on their respective first, second, third,… series are plotted against that series ordinal position, a peak of initial success is
followed by sharp reduction on the second and third series, whereafter the effect gradually
recovers to an asymptotic intermediate value over the higher series numbers [[Dunne, B. J., Dobyns, Y. H., Jahn, R. G., and Nelson, R. D. (1994). Series position effects in
random event generator experiments; With an Appendix by A.M. Thompson, “Serial position
effects in the psychological literature.” Journal of Scientific Exploration, Vol. 8, No. 2, p. 197.]]. This pattern
obtains, with minor disparities, for the overall HI, LO, and HI-LO data, but not for the baselines.
It also appears in a majority of the individual operator databases having five or more series. The
interpretation of this pattern on psychological or physical grounds can only be speculative at this
point, but its ubiquitous appearance clearly complicates any consistency or replicability criteria.

D. Distance and Time Dependence

The dependence of the effect sizes on the distance of the operator from the machine could
also be an important indicator of fundamental mechanism. Actually, no such dependence has
been found over the dimensions available in the laboratory itself. More remarkably, these
operator/machine aberrations continue to manifest in a substantial body of experiments wherein
operators are physically separated from the devices by distances of up to several thousand miles,
again with no statistically detectable dependence of the effect sizes on the degree of separation.
Rather, the results of some 396,000 trials per intention conducted under this “remote” protocol,
wherein the device is run unobserved at prearranged times by staff members who remain blind to
the operators’ intentions, are very similar in character to those of the local experiments, including
the scale of effect, and the relatively larger results under HI intentions compared to LO [[Dunne, B. J. & Jahn, R. G. (1992). Experiments in remote human/machine interaction. Journal of Scientific Exploration, Vol. 6, No. 4, p. 311.]].
In a subset of this remote database, comprising some 87,000 trials per intention, the
operators address their attention to the machine’s operation at times other than those at which the
data are actually generated. Such “off-time” experiments have ranged from 73 hours before to
336 hours after machine operation, and display a scale and character of anomalous results similar
to those of the locally generated data, including gender effects and count population distortions.
In fact, the overall mean shift in the high-intention efforts in these “off-time” remote experiments
is twice as large as that in the “on-time” remote data, although this difference is not statistically
significant, given the smaller size off-time database. As with the distance separations, no
dependence of the yield on the magnitude of the temporal separations is observed over the range
tested. Comparable remote and off-time results are found in the RMC experiment, as well.

E. Operator Strategy and Psychological Correlates

Although no systematic assessment of any of the multitude of potentially relevant
psychological parameters characterizing the operators has been attempted, on the basis of
informal discussions, casual observations of their styles, occasional remarks they record in the
experimental logbooks, and our own experiences as operators, it is clear that individual strategies
vary widely. Most operators simply attend to the task in a quiet, straightforward manner. A few
use meditation or visualization techniques or attempt to identify with the device or process in
some transpersonal manner; others employ more assertive or competitive strategies. Some
concentrate intently on the process; others are more passive, maintaining only diffuse attention to
the machine and diverting their immediate focus to some other activity, such as glancing through
a magazine, or listening to music. We find little pattern of correlation of such strategies with
achievement. Rather, the effectiveness of any particular operational style seems to be operatorspecific
and transitory; what seems to help one operator does not appeal to another, and what
seems to help on one occasion may fail on the next. If there is any commonality to be found in this diversity of strategy, it would be that the most effective operators tend to speak of the
devices in frankly anthropomorphic terms, and to associate successful performance with the
establishment of some form of bond or resonance with the device, akin to that one might feel for
one’s car, tools, musical instruments, or sports equipment.

V. Combined Results

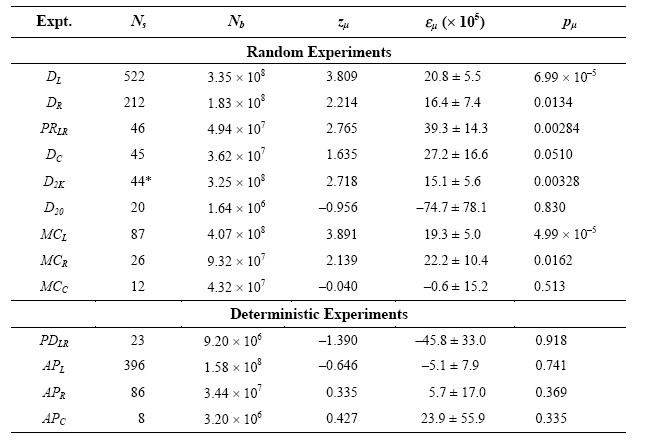
A summary of the results from all of the experimental excursions noted above, along with
a few others not specifically mentioned, is presented in Table 2. Listed here are the number of
complete experimental series,Ns; the number of binary samples processed, Nb; the z-scores based on the difference of the HI-LO means, zμ; the statistical effect sizes per bit, here reconstructed fromεμ, i.e., εμ = zμ/2

$\sqrtN_b$

), as discussed in Section III-A; and the one-tail probabilities associated
withzμ, pμ. Note that the table segregates those experiments having truly random sources from
those whose sources are deterministic pseudorandom. Of the former, only the two with the
smallest data sets fail to contribute positively to the overall HI-LO separation; in fact, all but
three independently achieve significance by thepμ< .05 criterion. In contrast, none of the
deterministic experiments show any correlations with operator intention, despite their identical
protocols and data processing, and their similar operator pools.
Combination of data from all of these experiments into an overall statistical figure of
merit is complicated by the major disparities in the various database sizes, some distinctions in
the protocols and measureables, the absence of theoretical expectations in the RMC experiments,
the pervasive gender disparities and the HI vs. LO asymmetries associated with them, and the
ambiguities associated with the interplay of series position effects with individual operator
database sizes. However, a number of meta-analytic techniques can be invoked to provide
composite estimates for the overall likelihood of the entire collection of anomalous mean shifts.
For example, one could simply compound the values ofzμlisted in Table 2 into an unweighted
composite value. Alternatively, one could weight the individual experimentzμvalues by the
numbers of series in the databases, or by the numbers of binary samples each contains. Finally,
one could combine results at the level of pμ values, rather thanzμ, using a method proposed by
Rosenthal [[Rosenthal, R. (1984). Meta-Analytic Procedures for Social Research. Beverly Hills, CA: SAGE
Publications, Inc.]]. In a separate paper, we have presented detailed arguments for preference of the
sample-weighted recipe for this type of data combination [[Dobyns, Y. H. (1996). “Drawing Conclusions from Multiple Experiments.” Technical Report
PEAR 96002, Princeton Engineering Anomalies Research, School of Engineering/Applied
Sciences, Princeton University.]] although, as displayed in Table 3,
the quantitative disparities among all of these methods are insufficient to obscure the magnitude
of the bottom-line results. Again note that by any of the recipes the ensemble of experiments
utilizing physically random sources compound to overwhelming statistical likelihood, while the
deterministic group lies well within chance expectation.
A similar sharp discrimination appears in both the composite series success rate and
operator success rate criteria. In the former, 58.4% of the total of 1014 random source
experimental series show a positive HI-LO separation (zs = 5.339, ps = 4.68 × 10-8), compared to
49.7% for the deterministic group (zs = -0.132, ps = 0.55). In the latter, 57.3% of the 199
operators of the random source experiments succeed in splitting their HI and LO results in the
intended direction (z0 = 2.056, p0 = 0.0199), compared to 45.7% of the 46 operators of the
deterministic group (z0 = -0.590, p0 = 0.722). By either criterion, the success rates are broadly
distributed over the various random source experiments, with eight of the nine contributing
positively to both the series and operator composites.
The strong distinction between the results using random and deterministic sources may
help discriminate among various theoretical models that have been proposed for effects of this
genre. For example, the “Decision Augmentation Theory” proposed by May et al. [[May, E. C., Utts, J. M., and Spottiswoode, S. J. P. (1995). Decision augmentation theory:
Applications to the random number generator database. Journal of Scientific Exploration, Vol. 9,
No. 4, p. 453.]], which
predicts that the nature of the source should be irrelevant to the presence or scale of the effect, is
clearly incompatible with this observed difference in performance. (A more detailed and
quantitative review of the implications of this database for the “D.A.T.” model can be found in
reference [[Dobyns, Y. H. & Nelson, R. D. (1997). “Empirical Evidence Regarding Decision Augmentation
Theory.” Technical Reort PEAR 97001, Princeton Engineering Anomalies Research, School of
Engineering/Applied Sciences, Princeton University.]]).

Table2.jpg
TABLE 2

VI. Replicability Requirements

From time to time, the experiments reported here have been assessed, both formally and
informally, by a number of critical observers, who have generally agreed that the equipment,
protocols, and data processing are sound [[National Research Council (1988). Enhancing Human Performance: Issues, Theories, and
Techniques. Report of the Committee on Techniques for the Enhancement of Human
Performance, Commission on Behavioral and Social Sciences and Education. Washington, DC:
National Academy Press.]]. Frequently, however, the caveat is added that
such results must be “replicated” before they can be fully accepted, with the replication criteria
variously defined to require strict preservation of all technical and procedural details, or to allow
more flexible similarities in equipment and protocols. It is our opinion that for experiments of
this sort, involving as they clearly do substantial psychological factors and therefore both
individual and collective statistical behaviors, to require that any given operator, on any given
day, should produce identical results, or that any given operator group should quantitatively
replicate the results of any other, is clearly unreasonable. Rather more apt would be such criteria
as might be applied to controlled experiments in human creativity, perception, learning, or
athletic achievement, where broad statistical ranges of individual and collective performance
must be anticipated, and results therefore interpreted in statistically generic terms.
By such criteria, the experiments outlined here can be claimed both to show internal
consistency, and to replicate results of similar experiments in many other laboratories. For
example, the statistical consistency of individual operator performances across multiple
experimental series that compound to their particular positions on Figure 4 defines one level of
internal replicability. The systematic accumulation of intention-correlated effects across many
operators, as displayed in Table 1, defines a second level. The consistently similar results of the
same group of operators on the various extensions of the basic REG experiment to other
protocols, noise sources, and categorically different random physical devices, shown in Table 3,
establishes a third, inter-experiment level of replicability.
With respect to inter-laboratory reproducibility, it should first be noted that the
experiments reported here were originally undertaken as an attempt to replicate previous studies
by Schmidt [[Schmidt, H. (1973). PK tests with a high-speed random number generator. Journal of
Parapsychology, Vol. 37, p. 105.]] and others [[Puthoff, H. & Targ, R. (1975). “Physics, Entropy, and Psychokinesis.” In L. Oteri, ed., Quantum
Physics and Parapsychology: Proceedings of an International Conference held in Geneva,
Switzerland, August 26-27, 1974. New York: Parapsychology Foundation, Inc.]], albeit with modifications in design and equipment that would
respond to various criticisms and allow more rapid accumulation of very large quantities of data.
Our results indeed reinforce this earlier work in confirming the existence, scale, and character of
anomalous correlations with pre-stated operator intentions. On a broader front, the previously
mentioned quantitative review of 30 years of research of this genre, covering more than 800
experiments reported by 68 principal investigators, including ourselves, concludes that despite
the historical improvement in experimental quality, a statistically constant anomalous effect size
has pervaded most of the results [[<33>]].

VII. Theoretical Modeling

Any attempts to model phenomena like those reported here must be immensely
complicated by the evidence that human volition is the primary correlate of the observed
anomalous physical effects, and thus that some proactive role for consciousness must somehow
be represented. This challenge is compounded by the absence of clear-cut psychological or
physiological indicators, and by the lack of demonstrable space and time dependence. While a
variety of attempts to combine conventional psychological and neurophysiological concepts with
established physical and mathematical formalisms, such as electromagnetic theory, statistical
thermodynamics, quantum mechanics, geophysical mechanics, and hyperspace formalisms have
been proposed [[Schmidt, H. (1973). PK tests with a high-speed random number generator. Journal of
Parapsychology, Vol. 37, p. 105.]], few of these propositions seem competent to accommodate the salient
features of the empirical data, let alone to survive critical scientific and epistemological criteria.
Rather, a more comprehensive approach to formulation of the interaction of
consciousness with the physical world seems requisite. Over the past two decades, a growing
number of theoretical physicists and philosophers of science have addressed the problem of
consciousness from this broader perspective, and have offered an assortment of more
sophisticated models which may eventually prove effective for dialogue with the empirical
results. Some of these apply quantum physical concepts and formalisms to neurological
processes and functions [[<28>]][[Consciousness Research Abstracts (1996). “Tuscon II: Toward a Science of Consciousness
1996.” Tucson, AZ, April 8-13, 1996. Thorverton, UK: Imprint Academic.]]. Others employ non-linear systems concepts underlying
information science, chaos, and complexity theories to provide degrees of freedom to
accommodate the intervention of consciousness into physical processes [[Atmanspacher, H. (1994). Complexity and meaning as a bridge across the Cartesian cut. Journal
of Consciousness Studies, Vol. 1, No. 2, p. 168.]]. Still others
propose a holistic complementarity between the epistemology of human experience and the
ontology of the physical world [[<37>]]. While each of these approaches at least acknowledges the
problem, the chasm between the role of consciousness and self-consistent physical theory is far
from bridged and, given its troublesome empirical and conceptual aspects, will require much
more visionary work from both the experimental and theoretical sides.

VIII. Extended Experiments

Since completion of the databases described above, a number of new experiments
involving substantially different physical processes, modes of feedback, and protocols have been
deployed in the hope of better identification of the most critical physical and psychological
properties bearing on the anomalous phenomena. For example, similar but more compact REG
units are being used to drive an “ArtREG” experiment, wherein two competing scenes are superimposed on a computer screen with relative illumination determined by the accumulating
balance of binary events from the noise source. The task of the operator is to cause one preselected
scene to dominate over the other, without current knowledge of the binary balance. In
another experiment, a compact REG drives a large musical drum to produce a random alternation
of equally spaced loud and soft beats or, in another variant, a random alternation of long and
short intervals of equal amplitude. The goal of the operator in either version is to impose some
regularity of pattern on the audible beat stream. Analysis programs compute the overall entropy
of the bit stream and search for repetitive sub-patterns indicative of an imposed cadence. Other
devices, such as classical single- and double-slit diffraction equipment, and REGs that alternate
digital and analog data sampling, or that compare two grossly different bit-sampling rates, help
search for further physical correlates. In a complementary effort to access the importance of
operator feedback modalities, various aesthetically engaging systems, such as a large linear
pendulum or an upward bubbling water fountain, have been employed, along with a mobile robot
driven in random motion by an on-board REG. Although the databases from these new
experiments are not yet sufficient to provide robust quantitative results, various anomalous
effects correlated with operator intention are apparent in the structural details of their data
distributions, of comparable scales to those seen in the direct REG interactions.

IX. Summary

The extensive databases described above, comprising more than 1500 complete
experimental series generated over a period of 12 years in rigid tripolar protocols by over 100
unselected human operators using several random digital processors, display the following
salient features:

  1. Strong statistical correlations between the means of the output distributions and the
    pre-recorded intentions of the operators appear in virtually all of the experiments
    using random sources.

  2. Such correlations are not found in those experiments using deterministic pseudorandom
    sources.

  3. The overall scale of the anomalous mean shifts are of the order of10
    -4

    bits per bit
    processed which, over the full composite database, compounds to a statistical
    deviation of more than7σ (p$\approx$3.5 × 10-13).

  4. While characteristic distinctions among individual operator performances are difficult
    to confirm analytically, a number of significant differences between female and male
    operator performance are demonstrable.

  5. The series score distributions and the count population distributions in both the
    collective and individual operator data are consistent with chance distributions based
    on slightly altered binary probabilities.

  6. Oscillatory series position patterns in collective and individual operator performance
    appear in much of the data, complicating the replication criteria.

  7. Experiments performed by operators far removed from the devices, or exerting their
    intentions at times other than that of device operation, yield results of comparable
    scale and character to those of the local, on-time experiments. Such remote, off-time
    results have been demonstrated on all of the random sources.

  8. Appropriate internal consistency, and inter-experiment and inter-laboratory replicability
    of the generic features of these anomalous results have been established.

  9. A much broader range of random-source experiments currently in progress display a
    similar scale and character of anomalous results.

Acknowledgments

The authors are deeply indebted to the many anonymous and uncompensated operators
who have unselfishly contributed immense time and effort to generation of the data on which this
study is based. We also appreciate the suggestions of many professional colleagues, both
supportive and critical, that have helped us refine and solidify these complex experiments.
This work has been supported in part by grants from the McDonnell Foundation, the
Ohrstrom Foundation, the Fetzer Institute, Mr. Laurance Rockefeller, Mr. Donald Webster, and
several other philanthropic organizations and individuals.

Publication originale :

Correlations of Random Binary Sequences with Pre-Stated Operator Intention: A Review of a 12-Year Program. J. Scientific Exploration, 11, No. 3, pp. 345-367, 1997.

La version PDF de cet article est disponible ici.

Site du PEAR :

http://www.princeton.edu/~pear/